sandeepsasi
Well-Known Member
Hello everyone,
This topic has been covered in several posts both in this forum and elsewhere. There are too many parameters involved and it can be really hard to come up with a one-size-fits-all solution and often, analysis has to be done on a case by case basis. However, I'm looking for a reasonable starting point, based on the common parameters specified for amps and speakers. For example, if I would like to try Rega's -R line-up for a speaker of my choice, generally regarded as easy to drive, should I choose Brio-R, Elex-R or Elicit-R? Most of the times, the answer given by the audiophile community,
"Go for Elicit-R if you can afford it. It is a kind of future proofing, have enough reserves of power for the lows, will easily drive any low-efficiency speaker that you may choose to buy in the future, has a superior power supply and output topology, ..."
is a bit vague, inclines towards more is always good philosophy and will just add to the confusion of a beginner like me, who's always on a budget. The Elex-R is roughly twice as expensive as Brio-R and Elicit-R costs about thrice, so all those benefits of Elicit-R over Brio-R comes at a cost. Here, I'm trying make an engineering estimate of what is the minimum power needed, to short list the amps first. Later, I can factor in sound quality and then, go one level up, if budget permits. If I really have the budget, I can even consider a better quality amp, both in terms of build and sound, from a different manufacturer, rated at a slightly higher than the minimum estimated power, but lower that the power rating of Elicit-R. In other words, I'm trying to find out where we stop paying for watts and start focusing on sound quality instead.
This discussion assumes that the speakers have already been finalized or someone is trying to find a match for a pair of speakers from a manufacturer's amp line-up. I've also come across cases where someone (a non-critical listener) is trying to upgrade their speakers, but would like to know whether their choice of speakers will match their current amps, as far as power is concerned.
Based on facts like doubling of distance will drop SPL by 6dB and doubling of amp power raises SPL by 3dB, I tried to quantify the well known relationship among amplifier power, speaker sensitivity and listening distance, in my own way. I would like to get my approach as well as the results reviewed by the experts here and also, would like to get a few questions, that I have myself, answered. To begin with, I'll quote a more specific version of the problem statement here:
I have a speaker of sensitivity S dB/W/m and of 8 Ohms nominal impedance rating and my listening position is at a distance D meters (m) from the speakers, so how much amplifier power, P in watts do I need?
This discussion is going to be a bit technical (highly objective) and there will be a few equations containing logarithms. My apologies for that. To come up with an equation for P, we definitely need more inputs:
1. How loud do we listen?
The way I understand, this can be quantified by SPL, at our listening position. Only problems is, the preferred SPL varies vastly from person to person. For example, I prefer listening at volumes low enough to have a conversation with someone sitting across the table, when I'm not alone at home. At the same time, I don't mind cranking up the volume if only my furry friend and I are there at home. Many people listen very loud, and as I've read on Troels Gravesen's website, the less distorting the system, the more is the tendency to listen louder without even realizing it. If we google "Safe SPL for music listening", a number that pops up is 85dB, which also says, safe only for less than 8 hours a day. I'll take this safe value as reasonable level, though I myself listen at much lower levels. Also, please note that this value can be customized as per your preferred listening levels.
2. What is the peak to average for the music I'm playing?
The average corresponds to the RMS value of the output amplitude, that we hear. This value must translate to 85dB of SPL that I've assumed in (1). However, what makes a system less distorting and highly musical is its ability to reproduce the peaks effectively. The amp must have enough power in reserve for the peaks in musical passages. The peak to average ratio decides the headroom needed for the peaks. Higher the ratio, more is the headroom needed. When DRC is used extensively to minimize this ratio, then this value tends to 1 and we can get away with very less headroom. This particular ratio varies significantly from track to track. So, once again, we may have to make an educated guess here. I have analyzed about 100 tracks due to demands at work (otherwise, why would I?), and have seen this ratio to be around 3. This is in agreement with the values for this ratio I've seen in textbooks and various forums. Giving more headroom, if we round-up this value to 4, then this translates to additional SPL of 20 * log10(4) or 12dB and a peak of SPL = 85dB + 12dB = 97dB.
The effect of distance
==============
As we move farther away from speakers, they start to sound quieter. To be specific, if we double the distance (2x) from the speakers, SPL drops by one-fourth (1/4x) or by 6dB, in logarithmic scale. For example, if the SPL of a speaker is rated at 90dB/W/m and we supply 1W of power to the speaker, the SPL at a distance of 1m from the speaker will be 90dB, 2m will be 84dB, 4m will be 78dB, and so on. We can take into account of this relationship, in logarithmic scale, by introducing a term 20 log10(D), where log10(x) is logarithm to the base 10 of x, and D is the distance from the speakers in meters and the factor of 2 in 20 takes care of inverse square law of distance.
The effect of power
=============
As we start cranking up the volume, the speakers start to get louder. To be specific, if we double the power to the speakers, the SPL also doubles or increases by 3dB. We can take into account of this relationship, in logarithmic scale, by introducing a term 10 log10(P).
So, to play music in its fully glory, we must target 97dB of SPL for the peaks, at our listening position, D meters away from the speakers. SPL is deteriorated by distance, as we move away from the speakers, and the amplifier must deliver more power to compensate for this. Speaker's sensitivity, S works in the favor of the amplifier, as highly sensitive speakers demand less power from the amp. Putting it all together,
10 log10(P) + S = 20 log10(D) + 97, or
10 log10(P) = 20 log10(D) + 97 - S
This is a first-order approximation, based on what I have understood.
3. Do we need to give additional headroom on top?
This varies from amp to amp. A few amplifiers are over designed and can be run at full volume without distortion. Entry level amps may go for modest choices of power supplies and output devices, and may start distorting when their power supplies run dry or their output devices are pushed to the boundaries of their linear regions, while delivering the peaks at full power. I'm considering entry level amps here, and am giving an additional head room of 10%. This means that, the power calculated from the previous equation should not exceed 90% of the output power of the amp, rated at 8 Ohms. The previous equation can be modified to take into account of this,
10 log10(P / 1.11) = 20 log10(D) + 97 - S,
where 1.11 = 100/90, for 10% headroom.
An example. My speakers have an SPL rating of 90dB/W/m and have a nominal impedance of 8 Ohms. My listening distance is about 2.39m. Substituting these values in the above equation, we get:
10 log10(P / 1.11) = 20 log10(2.39) + 97 - 90 = 14.568
P = 1.11 * 10^(14.568 / 10) = 31.78W (The operation 10^y, means 10 to the power y, or antilog to the base 10 of y)
If I ever decide to purchase an amp from the the Rega -R series, then I will start with Brio-R and may even consider Elex-R, but Elicit-R will definitely be a stretch, as far as power is concerned. Once again, this comment is purely based on power, and how these amps sound and their synergy with my speakers, and rest of the chain, is a different topic altogether. Next, we'll try to address point (4).
4. What if the rated nominal impedance of my speakers is 4 Ohms or there is a large impedance dip at certain frequencies?
If the nominal impedance of the speakers is 4 Ohms, then the power calculated by the previous equation must also be doubled for an ideal amp, i.e., an ideal amp will double its power when the impedance is halved. Speakers don't present a constant impedance to the amp at all frequencies. To ensure that the amp does not run out of juice at these impedance dips, we have to make sure that the amp can supply sufficient power at the worst impedance value, which is the minimum impedance. A few manufacturers make our life simple by quoting the minimum impedance of speakers, at a certain frequency. We can cover both the cases of 4 Ohms speakers as well as impedance dips, by introducing a term 10 log10(8 / Rmin) in our equation, where Rmin is the minimum impedance of the speaker in Ohms. Thus, the modified equation is now,
10 log10(P / 1.11) = 20 log10(D) + 97 - S + 10 log10(8 / Rmin)
For speakers having a nominal impedance of 4 Ohms, put Rmin = 4, to calculate the minimum power at nominal impedance. Also, note that this term reduces to zero, if you put Rmin = 8. It can also be verified that the power at 4 Ohms is double that of the the power at 8 Ohms, using the above equation.
By bringing Rmin to the equation, we'll have more things to worry about. Not all amplifiers can double their power when impedance is halved. In fact, many amps (Rega -R series, Marantz PM8006, Luxman-505uX II, and a few others on hifimart.com for which this data is available), can only increase their output power by 1.5x, when the impedance is halved from 8 Ohms to 4 Ohms. If the minimum impedance, Rmin, is in the ballpark of 4 Ohms, then we will have to consider an amplifier that can drive 4 Ohm loads and for which this data is explicitly specified by the manufacturer. If no data is available, it's quite possible that the amp is not designed to handle 4 Ohms speakers. Also, in these cases, we will have to compare the power estimated by the equation against the power rating of the amplifier at 4 Ohms, rather than 8 Ohms.
Notes:
====
1. I found this equation as a way of checking whether a speaker is too big for our room. A few manufacturers provide a spec called recommended minimum amplifier power. This is said to be the minimum power at which the speakers start to sound their best. If this power turns out to be much higher than what is estimated by the above equation, then it could be a sign that the speakers could be too big for our room. For eg, Monitor Audio Silver 500 speakers have a recommended minimum amp power rating of 80W. Given, a sensitivity of 90dB/W/m and nominal impedance of 8 Ohms, the minimum power required to produce 97dB of SPL at my listening position is only 32W. If I ever attempt to pump 80W at 8 Ohms to these speakers at home, I expect somebody from hifivision.com to bail me out of "domestic violence by noise pollution" charges. This speaker is also an interesting speaker in that it's minimum impedance dips to 3.1 Ohms at 2.45kHz, which means we'll be needing to pair an amp capable of driving 4 Ohm loads, with these speakers and the amp should be rated at least 82W at 4 Ohms.
Questions:
=======
1. Is there anything like a stereo reinforcement? When we play stereo, the SPL at the listening position is produced by two speakers, combined. Do we have to modify the equation to take account of this?
2. How do we exactly measure the listening distance?
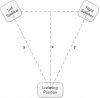
Is it x or y, in the above figure? It is 7.83 feet v/s 7 feet in my listening room; so, irrespective of which value I choose, the calculated power doesn't vary a lot.
With regards,
Sandeep Sasi
This topic has been covered in several posts both in this forum and elsewhere. There are too many parameters involved and it can be really hard to come up with a one-size-fits-all solution and often, analysis has to be done on a case by case basis. However, I'm looking for a reasonable starting point, based on the common parameters specified for amps and speakers. For example, if I would like to try Rega's -R line-up for a speaker of my choice, generally regarded as easy to drive, should I choose Brio-R, Elex-R or Elicit-R? Most of the times, the answer given by the audiophile community,
"Go for Elicit-R if you can afford it. It is a kind of future proofing, have enough reserves of power for the lows, will easily drive any low-efficiency speaker that you may choose to buy in the future, has a superior power supply and output topology, ..."
is a bit vague, inclines towards more is always good philosophy and will just add to the confusion of a beginner like me, who's always on a budget. The Elex-R is roughly twice as expensive as Brio-R and Elicit-R costs about thrice, so all those benefits of Elicit-R over Brio-R comes at a cost. Here, I'm trying make an engineering estimate of what is the minimum power needed, to short list the amps first. Later, I can factor in sound quality and then, go one level up, if budget permits. If I really have the budget, I can even consider a better quality amp, both in terms of build and sound, from a different manufacturer, rated at a slightly higher than the minimum estimated power, but lower that the power rating of Elicit-R. In other words, I'm trying to find out where we stop paying for watts and start focusing on sound quality instead.
This discussion assumes that the speakers have already been finalized or someone is trying to find a match for a pair of speakers from a manufacturer's amp line-up. I've also come across cases where someone (a non-critical listener) is trying to upgrade their speakers, but would like to know whether their choice of speakers will match their current amps, as far as power is concerned.
Based on facts like doubling of distance will drop SPL by 6dB and doubling of amp power raises SPL by 3dB, I tried to quantify the well known relationship among amplifier power, speaker sensitivity and listening distance, in my own way. I would like to get my approach as well as the results reviewed by the experts here and also, would like to get a few questions, that I have myself, answered. To begin with, I'll quote a more specific version of the problem statement here:
I have a speaker of sensitivity S dB/W/m and of 8 Ohms nominal impedance rating and my listening position is at a distance D meters (m) from the speakers, so how much amplifier power, P in watts do I need?
This discussion is going to be a bit technical (highly objective) and there will be a few equations containing logarithms. My apologies for that. To come up with an equation for P, we definitely need more inputs:
- How loud do we listen? This varies significantly from person to person
- What is the peak to average for the music we're playing? This will help us decide how much additional headroom we need for the peaks. To get the exact ratio, we really have to do a statistical analysis of our entire music collection
- Do we need to account for additional headroom on top of this? As a rule of thumb, it is always better not to run entry level integrated amps at full volume setting
- What if the rated nominal impedance of my speakers is 4 Ohms or there is a large impedance dip at certain frequencies? With watts getting cheaper, modern speakers take power for granted and a speaker having a nominal impedance rating of 8 Ohms can have it's impedance dip to 4 ohms or lower at certain frequencies
- Are our speakers really as efficient as claimed by the manufacturer?
- Do we need to consider additional effects like room absorption, reflection, etc?
- ...
1. How loud do we listen?
The way I understand, this can be quantified by SPL, at our listening position. Only problems is, the preferred SPL varies vastly from person to person. For example, I prefer listening at volumes low enough to have a conversation with someone sitting across the table, when I'm not alone at home. At the same time, I don't mind cranking up the volume if only my furry friend and I are there at home. Many people listen very loud, and as I've read on Troels Gravesen's website, the less distorting the system, the more is the tendency to listen louder without even realizing it. If we google "Safe SPL for music listening", a number that pops up is 85dB, which also says, safe only for less than 8 hours a day. I'll take this safe value as reasonable level, though I myself listen at much lower levels. Also, please note that this value can be customized as per your preferred listening levels.
2. What is the peak to average for the music I'm playing?
The average corresponds to the RMS value of the output amplitude, that we hear. This value must translate to 85dB of SPL that I've assumed in (1). However, what makes a system less distorting and highly musical is its ability to reproduce the peaks effectively. The amp must have enough power in reserve for the peaks in musical passages. The peak to average ratio decides the headroom needed for the peaks. Higher the ratio, more is the headroom needed. When DRC is used extensively to minimize this ratio, then this value tends to 1 and we can get away with very less headroom. This particular ratio varies significantly from track to track. So, once again, we may have to make an educated guess here. I have analyzed about 100 tracks due to demands at work (otherwise, why would I?), and have seen this ratio to be around 3. This is in agreement with the values for this ratio I've seen in textbooks and various forums. Giving more headroom, if we round-up this value to 4, then this translates to additional SPL of 20 * log10(4) or 12dB and a peak of SPL = 85dB + 12dB = 97dB.
The effect of distance
==============
As we move farther away from speakers, they start to sound quieter. To be specific, if we double the distance (2x) from the speakers, SPL drops by one-fourth (1/4x) or by 6dB, in logarithmic scale. For example, if the SPL of a speaker is rated at 90dB/W/m and we supply 1W of power to the speaker, the SPL at a distance of 1m from the speaker will be 90dB, 2m will be 84dB, 4m will be 78dB, and so on. We can take into account of this relationship, in logarithmic scale, by introducing a term 20 log10(D), where log10(x) is logarithm to the base 10 of x, and D is the distance from the speakers in meters and the factor of 2 in 20 takes care of inverse square law of distance.
The effect of power
=============
As we start cranking up the volume, the speakers start to get louder. To be specific, if we double the power to the speakers, the SPL also doubles or increases by 3dB. We can take into account of this relationship, in logarithmic scale, by introducing a term 10 log10(P).
So, to play music in its fully glory, we must target 97dB of SPL for the peaks, at our listening position, D meters away from the speakers. SPL is deteriorated by distance, as we move away from the speakers, and the amplifier must deliver more power to compensate for this. Speaker's sensitivity, S works in the favor of the amplifier, as highly sensitive speakers demand less power from the amp. Putting it all together,
10 log10(P) + S = 20 log10(D) + 97, or
10 log10(P) = 20 log10(D) + 97 - S
This is a first-order approximation, based on what I have understood.
3. Do we need to give additional headroom on top?
This varies from amp to amp. A few amplifiers are over designed and can be run at full volume without distortion. Entry level amps may go for modest choices of power supplies and output devices, and may start distorting when their power supplies run dry or their output devices are pushed to the boundaries of their linear regions, while delivering the peaks at full power. I'm considering entry level amps here, and am giving an additional head room of 10%. This means that, the power calculated from the previous equation should not exceed 90% of the output power of the amp, rated at 8 Ohms. The previous equation can be modified to take into account of this,
10 log10(P / 1.11) = 20 log10(D) + 97 - S,
where 1.11 = 100/90, for 10% headroom.
An example. My speakers have an SPL rating of 90dB/W/m and have a nominal impedance of 8 Ohms. My listening distance is about 2.39m. Substituting these values in the above equation, we get:
10 log10(P / 1.11) = 20 log10(2.39) + 97 - 90 = 14.568
P = 1.11 * 10^(14.568 / 10) = 31.78W (The operation 10^y, means 10 to the power y, or antilog to the base 10 of y)
If I ever decide to purchase an amp from the the Rega -R series, then I will start with Brio-R and may even consider Elex-R, but Elicit-R will definitely be a stretch, as far as power is concerned. Once again, this comment is purely based on power, and how these amps sound and their synergy with my speakers, and rest of the chain, is a different topic altogether. Next, we'll try to address point (4).
4. What if the rated nominal impedance of my speakers is 4 Ohms or there is a large impedance dip at certain frequencies?
If the nominal impedance of the speakers is 4 Ohms, then the power calculated by the previous equation must also be doubled for an ideal amp, i.e., an ideal amp will double its power when the impedance is halved. Speakers don't present a constant impedance to the amp at all frequencies. To ensure that the amp does not run out of juice at these impedance dips, we have to make sure that the amp can supply sufficient power at the worst impedance value, which is the minimum impedance. A few manufacturers make our life simple by quoting the minimum impedance of speakers, at a certain frequency. We can cover both the cases of 4 Ohms speakers as well as impedance dips, by introducing a term 10 log10(8 / Rmin) in our equation, where Rmin is the minimum impedance of the speaker in Ohms. Thus, the modified equation is now,
10 log10(P / 1.11) = 20 log10(D) + 97 - S + 10 log10(8 / Rmin)
For speakers having a nominal impedance of 4 Ohms, put Rmin = 4, to calculate the minimum power at nominal impedance. Also, note that this term reduces to zero, if you put Rmin = 8. It can also be verified that the power at 4 Ohms is double that of the the power at 8 Ohms, using the above equation.
By bringing Rmin to the equation, we'll have more things to worry about. Not all amplifiers can double their power when impedance is halved. In fact, many amps (Rega -R series, Marantz PM8006, Luxman-505uX II, and a few others on hifimart.com for which this data is available), can only increase their output power by 1.5x, when the impedance is halved from 8 Ohms to 4 Ohms. If the minimum impedance, Rmin, is in the ballpark of 4 Ohms, then we will have to consider an amplifier that can drive 4 Ohm loads and for which this data is explicitly specified by the manufacturer. If no data is available, it's quite possible that the amp is not designed to handle 4 Ohms speakers. Also, in these cases, we will have to compare the power estimated by the equation against the power rating of the amplifier at 4 Ohms, rather than 8 Ohms.
Notes:
====
1. I found this equation as a way of checking whether a speaker is too big for our room. A few manufacturers provide a spec called recommended minimum amplifier power. This is said to be the minimum power at which the speakers start to sound their best. If this power turns out to be much higher than what is estimated by the above equation, then it could be a sign that the speakers could be too big for our room. For eg, Monitor Audio Silver 500 speakers have a recommended minimum amp power rating of 80W. Given, a sensitivity of 90dB/W/m and nominal impedance of 8 Ohms, the minimum power required to produce 97dB of SPL at my listening position is only 32W. If I ever attempt to pump 80W at 8 Ohms to these speakers at home, I expect somebody from hifivision.com to bail me out of "domestic violence by noise pollution" charges. This speaker is also an interesting speaker in that it's minimum impedance dips to 3.1 Ohms at 2.45kHz, which means we'll be needing to pair an amp capable of driving 4 Ohm loads, with these speakers and the amp should be rated at least 82W at 4 Ohms.
Questions:
=======
1. Is there anything like a stereo reinforcement? When we play stereo, the SPL at the listening position is produced by two speakers, combined. Do we have to modify the equation to take account of this?
2. How do we exactly measure the listening distance?

Is it x or y, in the above figure? It is 7.83 feet v/s 7 feet in my listening room; so, irrespective of which value I choose, the calculated power doesn't vary a lot.
With regards,
Sandeep Sasi

