That is a great point koushik which never struck me till you pointed it out. Digital music is always LOSSY. Digital music can never be LOSSLESS. You are always loosing music between each sample.
So assuming that today we have the technology to sample at upto 1MHz (theoretically it can be infinite) but for argument sake let's limit ourselves to current technology. A CD is sampled at 44Khz would loose a whopping 95.6% of music, only 4.4% of the music is captured on a CD.
A Flac at 96 KHz would loose about 90% and Flac at 192 KHz would loose 80%.
Whereas in a pure Analog path no music is theoretically

lost.
Just my theory , what do you guys think ? Is my math right ?
Wrong.
1. When we talk about loss, we are not concerned with simply how much of the high frequency spectrum has been chopped off, BUT we are concerned with how much of the information was actually present in the high frequency spectrum that was audible which was chopped off.
When I show you a picture (whether film or digital) I have chopped off all the ultra-voilet and infra-red spectrum. Spectrum wise visible light is a VERY NARROW band - using your mathematics it seems as if I have LOST all the signal because I have not include UV and IR spectrum in my photos!
Well we might have lost the UV and IR, but it makes no difference to our eyes.
2. It is wrong to say that analog signal is 100% complete. Perhaps it is 100% complete - but would you want to listen to a 100% complete signal, without knowing that you are actually listening to 100 MHz ultrasonic noise.
The SNR at each frequency is a very important criteria - and analog signals are very poor at high frequencies (because of physics). I am sure you are aware what the grooves in the LP disc represent. The higher the frequencies - the closer theundulations in the grooves are. The closer the undulations are - the more difficult it is to (a) produce the tracks accurately (b) keep the grooves static free - due to small foreign particles (c) reproduce the running groove and convert it back to electrical signal
So I ask my question again - would you be happy listening to 100% complete audio signal - knowing fully well the high end of the spectrum has pretty poor SNR and thus filled with noise.
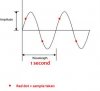
3. This is not in response to your post, but Shannon Nyquist sampling rate theorem is actually very intuitive once you put your brain on it. (T.E.G. - no maths involved!) Picture at the end of post.
Let say there is a 1 Hz sine wave. If I sample it at twice frequency = 2 Hz (which means two times a second), I will encounter two points every second.
Fine? (which two points - will depend on where I start the sampling - but the fact remains that these two points will remain fixed over all the sine wave cycles).
Now, try to imagine all the sort of sine waves that you can pass through these red points.
You will realize the the ONLY sine waves that you can pass through ALL these red dots will be the sine waves with frequency equal to or higher than 1 Hz!
... and any frequency lower than 1 Hz will miss some or the other red points.
SO, its only the sine wave with freq = 1 Hz that can fit the red points perfectly.
This means that in order to sample a sine wave perfectly - you need to sample it at twice the signal frequency - and it can be reproduced perfectly.
This is exactly what Shannon Nyquist theorem speaks about in mathematical terms.
There might be a few questions lingering.
a)
But you just said that "You will realize the the ONLY sine waves that you can pass through ALL these red dots will be the sine waves with frequency equal to or higher than 1 Hz!"
Yes, but our system can understand, and replicate all frequencies UPTO 1 Hz. Nothing higher than that. So we don't even care if higher frequency sine waves can fit the red dots.
b)
Fine, but you are only talking about sine waves. What about "complex" weird wave forms encountered in the Classical music.
Any wave form can be perfectly represented as an series of sine waves (or cosine waves if you like). In simple terms a complex waveform can be represented as a superposition (addition/subtraction) of more than one sine wave.
c)
What about transients in acoustics?
Well lets take a sine wave, and chop it so that we are looking at the rising part. What is this rising part? This is the transient. (For 22050 Hz sine wave, the wavelength = 45.3 microseconds. Therefore the first rising part = 45.3/4 = 11.3 s)
So as long as the transient is more than 11.3 s, it will be captured perfectly by our digitally sampled signal.
d)
So what happens about transients that are faster than 1 s?
If you can listen to such transients - it simply means that you can listen to frequencies 10 times higher than 22 kHz.
lost.